Understanding Big O Time Complexity: A Comprehensive Guide with Examples

Big O notation is a mathematical concept used in computer science to describe the time complexity of an algorithm. In simple terms, it represents how quickly the algorithm's running time grows with the size of the input.

The notation is represented by the letter "O" followed by a mathematical function. For example, O(n) represents an algorithm whose running time increases linearly with the size of the input, while O(n^2) represents an algorithm whose running time increases quadratically with the input size.

In this blog post, we'll explore the concept of Big O notation in more detail, including its definition, how it is used, and some examples to help you better understand it.

Definition of Big O Notation

Big O notation is used to describe the upper bound of the running time of an algorithm. In other words, it describes the worst-case scenario of an algorithm's performance.

To understand this, let's take an example. Consider the following algorithm that searches for a particular element in an array:

public static boolean search(int[] array, int target) {
    for (int element : array) {
        if (element == target) {
            return true;
        }
    }
    return false;
}

In this algorithm, the worst-case scenario is when the target element is not present in the array. In that case, the algorithm will have to search through the entire array, resulting in a running time proportional to the size of the array, which we denote as O(n).

The O(n) notation indicates that the running time of the algorithm increases linearly with the size of the input.

Similarly, consider the following algorithm that searches for all pairs of elements in an array:

public static void searchPairs(int[] array) {
    for (int i = 0; i < array.length; i++) {
        for (int j = i + 1; j < array.length; j++) {
            System.out.println(array[i] + " " + array[j]);
        }
    }
}

In this case, the algorithm will have to search through all pairs of elements in the array, resulting in a running time proportional to the square of the size of the array, which we denote as O(n^2).

The O(n^2) notation indicates that the running time of the algorithm increases quadratically with the size of the input.

How Big O Notation is Used ?

Big O notation is used to analyze the performance of algorithms and to compare different algorithms. It helps in determining the efficiency of an algorithm and whether it is suitable for a particular problem.

For example, suppose you have two algorithms that solve the same problem, but one has a time complexity of O(n) and the other has a time complexity of O(n^2). In that case, you would choose the algorithm with O(n) time complexity since it will be more efficient for larger input sizes.

Big O notation also helps in understanding the scalability of an algorithm. Scalability refers to an algorithm's ability to handle larger input sizes without a significant increase in running time. An algorithm with a time complexity of O(n) is more scalable than an algorithm with a time complexity of O(n^2).

Examples of Big O Notation

Let's take a look at some common examples of algorithms and their time complexities:

1. Constant time complexity O(1)

An algorithm with constant time complexity takes the same amount of time to execute, regardless of the size of the input. For example, accessing an element in an array takes constant time, since the position of the element can be calculated directly from the index:

public static int access(int arr[],int index){
    return arr[index];
}

1. Linear time complexity O(n)

An algorithm with linear time complexity takes a time proportional to the size of the input. For example, searching for an element in an unsorted array takes linear time, since each element must be checked in turn:

public int search(int arr[],int index){    
    for(int ele:arr){
        if (ele==target){
            return true;    
            }        
    }
return false;
}

3. Quadratic time complexity O(n^2)

An algorithm with quadratic time complexity takes a time proportional to the square of the size of the input. For example, sorting an array using a bubble sort algorithm takes quadratic time, since each element must be compared with every other element:

public static void bubbleSort(int[] array) {
    int n = array.length;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (array[j] > array[j+1]) {
                int temp = array[j];
                array[j] = array[j+1];
                array[j+1] = temp;
            }
        }
    }
}

4. Exponential time complexity (O(2^n))

An algorithm with exponential time complexity takes a time proportional to 2 raised to the power of the size of the input. For example, finding all possible subsets of an array takes exponential time, since each element can either be included or excluded, resulting in a total of 2^n possible subsets:

import java.util.ArrayList;
import java.util.List;

public static List<List<Integer>> subsets(List<Integer> array) {
    if (array.size() == 0) {
        List<List<Integer>> result = new ArrayList<>();
        result.add(new ArrayList<>());
        return result;
    } else {
        int element = array.remove(array.size() - 1);
        List<List<Integer>> subsetsWithoutElement = subsets(array);
        List<List<Integer>> subsetsWithElement = new ArrayList<>();
        for (List<Integer> subset : subsetsWithoutElement) {
            List<Integer> subsetWithElement = new ArrayList<>(subset);
            subsetWithElement.add(element);
            subsetsWithElement.add(subsetWithElement);
        }
        subsetsWithoutElement.addAll(subsetsWithElement);
        return subsetsWithoutElement;
    }
}

5. Logarithmic time complexity O(log n)

An algorithm with logarithmic time complexity takes a time proportional to the logarithm of the size of the input. For example, searching for an element in a sorted array using a binary search algorithm takes logarithmic time, since each comparison reduces the search space by half:

public static void bSearch(int arr[],int target){
    int start=0;
    int end=arr.length-1;

    while(start<end){
    int mid=start+(end-start)/2;
        if (array[mid] == target) {
            return true;
        } else if (array[mid] < target) {
            start = mid + 1;
        } else {
            end = mid - 1;
        }
    }
    return false;

}

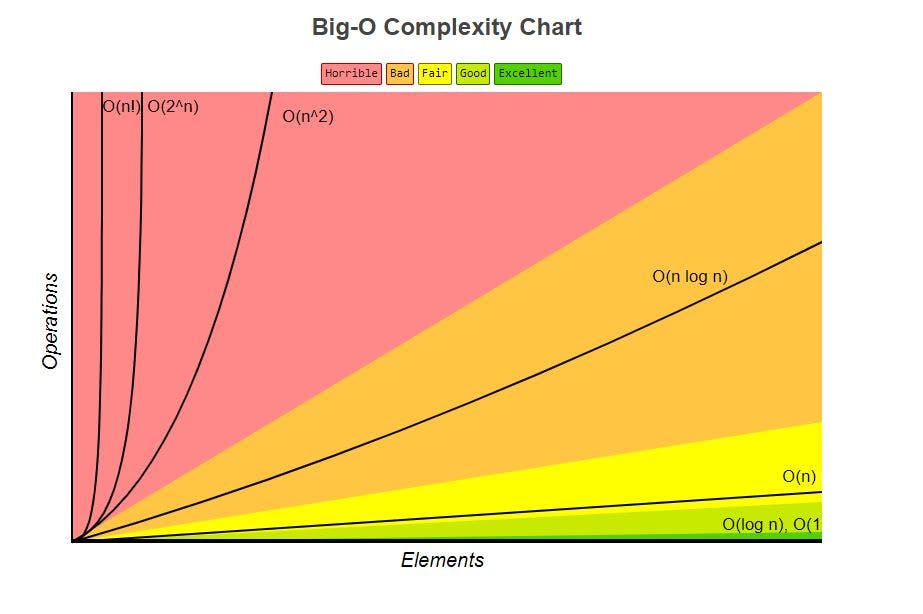
Big-O Complexity Chart

The Big O time complexity chart is a graph that shows the performance of different algorithms as the input size increases. The horizontal axis represents the input size, which can be expressed in terms of the number of items to be sorted, searched, or processed. The vertical axis represents the running time of the algorithm, measured in terms of the number of operations performed by the algorithm.

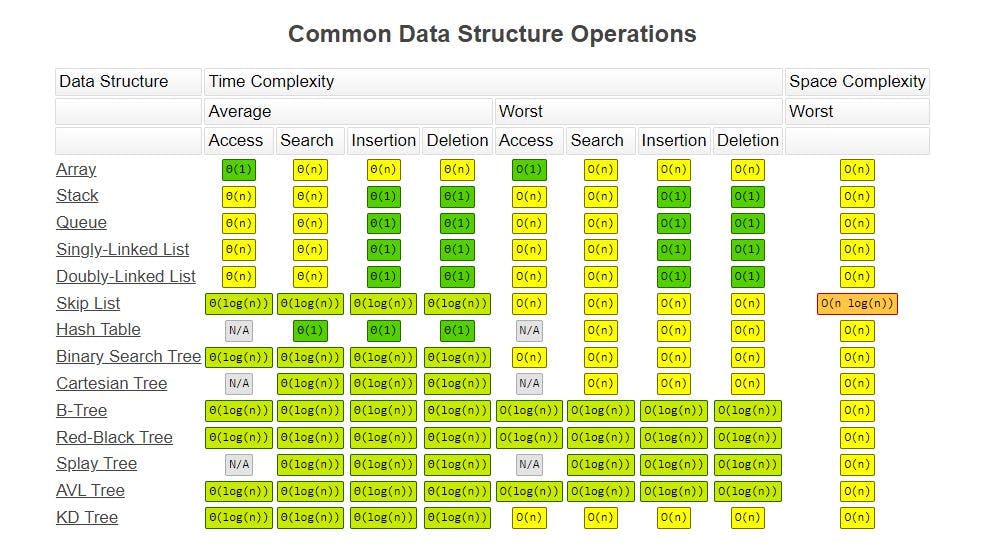
Common Data-Structures Operations

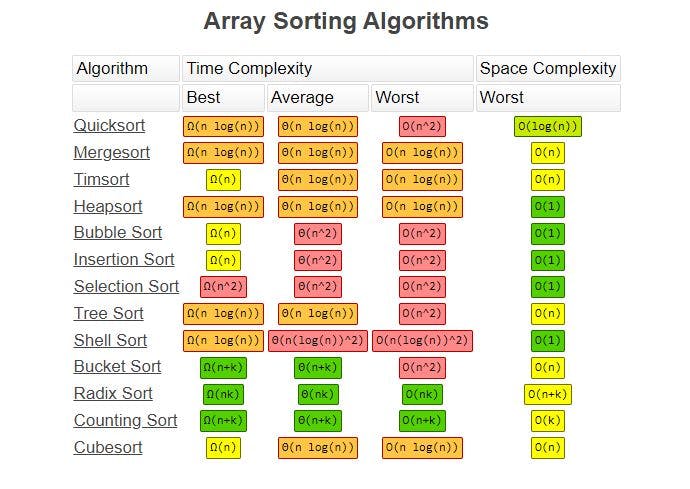
Array Sorting Algorithms

Conclusion

Big O notation is a powerful tool used to describe the time complexity of algorithms. It helps in determining the efficiency and scalability of an algorithm and is used to compare different algorithms for a particular problem. By understanding the time complexity of algorithms, you can write more efficient and scalable code and make informed decisions about which algorithm to use for a given task.